Blenderのシェーダーで Voronoi Texture(ボロノイテクスチャ) はよく使われるテクスチャノードだと思います。
ノイズとは違うセル状の模様を簡単に作れる便利なテクスチャですが、実はモードやパラメータによって、傾向の異なるパターンを生成できる ことはご存じでしょうか?
雰囲気で触っていてもどんな形ができるのか予測しづらくて使いにくいと思ってる方も多いかもしれませんが、ボロノイテクスチャでできるパターンには、ある点からの距離でできるセルという原理・ルールがあります。これらの原理や、生成されやすい形を理解することでボロノイテクスチャへの解像度が一段階確実に上がります。
この記事では、Voronoi Textureの各モードの特徴を、図(パターン例)や計算式の説明をまじえながら分かりやすく解説します。
- 距離関数・空間(ボロノイテクスチャノードでできるパターンの原理のルール)の説明
- どのモードでどんな模様が作れるのか
- Randomness(ランダム)、Smoothness(スムーズネス)などパラメータの効果
- ボロノイテクスチャで作れるテクスチャ応用例
まで、深堀りしています。
「とりあえずVoronoiを使ってみたけど、なんかよく分からない」という方でも、この記事を読み終えるころには 思い通りの模様を作れるようになる!!… はずです。プロシージャルな形、パターンの生成に欠かせないテクスチャですのでぜひ参考にしてみてください。
この記事は、BlenderのVoronoi Textureノードを解説している初級者~中級者向けの記事です。
難易度
Voronoi Textureとは?
ボロノイテクスチャノードは調整する項目が多く、それが使いづらさにつながっています。通常のパラメータに加え、モードが3つもあり、それぞれのモードにいくつも選択肢があるからです。そしてそれらの組み合わせによってでパターンのベースが生成され、さらにパラメータでその形を変形することができるからです。
今回はまず大まかにボロノイテクスチャのモードの説明をし、F1,F2などのFeature (特徴出力)モード、それからパラメータを紹介します。そして、一番わかりにくいであろうDistance Metric (距離関数)(Euclidean, Manhattanなど)のモードについて解説しています。
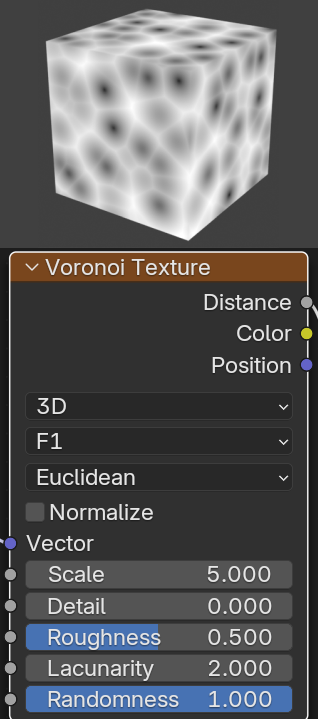
Voronoi Textureの大体
- 隣接する点(セルポイント)との距離から模様を作るテクスチャ
- ノイズよりも幾何学的で、細胞・ひび割れ・石壁・破片のような模様に向いている
- Cycles/Eeveeどちらでも同じ動き
複数のモードがある
ボロノイテクスチャノードにはパラメータの上に3つのモード選択欄があります。各モードを上から大まかに解説します。Feature (特徴出力)とDistance Metric (距離関数)などわかりにくい箇所はまた下記で詳細に解説しています。
- Dimensions(次元)
- 1D…1次元。出力値は1つの値になる。色なら1色しか出ない。
- 2D…2次元。平面(例えばXY平面)にはパターンが出力され、同じ模様の板が Z 方向に無限に積み重なっているようになっている。平面方向にしか動きの変化はない。
- 3D…3次元。3次元方向すべてにパターンが出力される。
- 4D…4次元。3次元方向すべてにパターンが出力され、変化する。それにプラスでWというパラメータが出来て、パターンの様相が伸び縮みするように変化する。下記の波模様の場合、時間が経って波が動いてるような動きになる。
※高次元になるほどレンダリングが重くなります。高次元が必要でない限り低次元を使用した方がいいです。

- Feature (特徴出力)…ノードが計算する距離の種類
- F1:最も近い特徴点までの距離、その位置、および色。
- F2:2 番目に近い特徴点までの距離、その位置、および色。
- Smooth F1:F1 のスムーズバージョン。
- Distance to Edge (端との距離):Voronoi セルの境界までの距離。
- N-Sphere Radius (N球面半径):Voronoi セルに内接する n 次元球の半径。つまり、最も近い特徴点と、その次に近い特徴点との距離の半分です。
- Distance Metric (距離関数)…テクスチャの計算に使用される距離空間(距離の計算方法)。
- Euclidean (ユークリッド):ユークリッド距離を使用します。
- Manhattan (マンハッタン距離):マンハッタン距離を使用します。
- Chebychev (チェビシェフ距離):チェビシェフ距離を使用します。
- Minkowski (ミンコフスキー):ミンコフスキー距離を使用します。ミンコフスキー距離は、Exponent(指数) をパラメータとして使用する、前述の距離メトリックの一般形です。
- 指数 1 → Manhattan 距離
- 指数 2 → Euclidean 距離
- 指数 → ∞(非常に大きい値) → Chebychev 距離
※Feature, Distance Metricについては各セクションで詳細に解説しています。
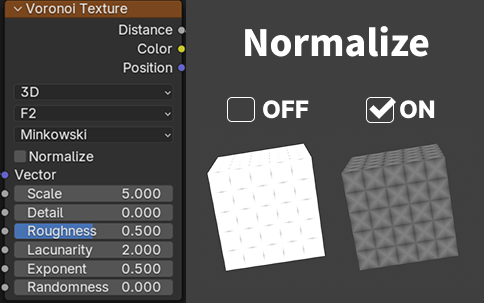
Normalize (正規化)
有効にすると、出力値が 0.0 〜 1.0 の範囲に収まるようにします。
デフォルトはOFF
大体の出力は0~1の間に収まっていますが、まれに、Feature が F2 の場合、0〜1 の範囲外になることがあります。そういうときにNormalizeをONにすると出力がきちんと出るようになります。
出力
Dimensions(次元)やFeature (特徴出力)によって出力できる値が変わってきます。出力値は以下のものがあります。
- Distance
- Color
- W
- Position
- Radius
詳しくは以下のFeature (特徴出力)で解説しています。
ノードの設定、特に Randomness の値が低い場合、レンダリングアーティファクトが発生することがあるとマニュアルに書いてあります(自分は遭遇したことはないです)。
Feature (特徴出力)
Voronoi Textureノードの出力タイプ(Distance/Positionなど)を選ぶモードで、セルのパターンを作るため、「何の距離を計算して出力するか」を指定しています。
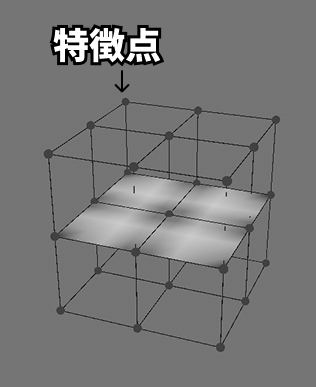
Voronoiでいう特徴点
Voronoi Texture は空間内に ランダムに配置された点(特徴点) を置きます。これらの点を基準に、各点から最も近い特徴点までの距離でセルを分けます。つまり、特徴点 = セルの核(中心)になる点 です。
ランダム値を増やすとこの特徴点の場所がランダムに散ります。
F1
最も近い特徴点までの距離でVoronoiセルを作ります。
出力はDistance, Color, Positionがあります。
- Distance…最も近い特徴点までの距離を値で出す
- Color…セルの識別用に使えるランダムな色が出力されます。
- Position…テクスチャ座標に従ってPositionに対応したベクトル、色が出力されます。
- W(1Dと4Dのときのみ)…特徴点の位置のベクトル。ランダムなどで位置をずらさないと、ある1つの値しか出ない。

F2
2番目に近い特徴点までの距離でVoronoiセルを作ります。セルの形は三角形になります(2D、ランダムが0の場合)
出力はDistance, Color, Positionがあります。
- Distance…2番目に近い特徴点までの距離を値で出す(例えば右図の白のバッテンの中心に特徴点はあるのですが、点aの場合、その場の特徴点ではなく隣の特徴点までの距離を出さなければなりません。点bの場合上下の特徴点の遠い方の距離を出します。)
- Color…セルの識別用に使えるランダムな色が出力されます。
- Position…テクスチャ座標に従ってPositionに対応したベクトル、色が出力されます。
- W(1Dと4Dのときのみ)…特徴点の位置のベクトル。ランダムなどで位置をずらさないと、ある1つの値しか出ない。

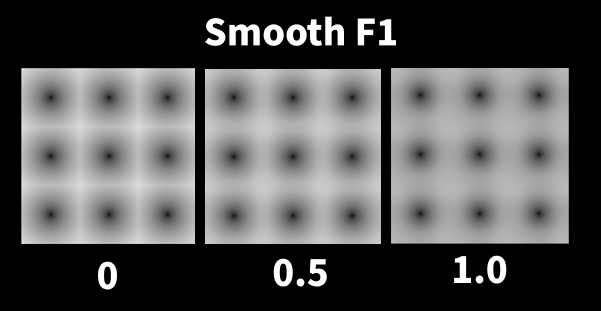
Smooth F1
F1 のスムーズバージョン。セルの境界を滑らかにブレンドしています。
出力はDistance, Color, Positionがあります。

Distance to Edge(端までの距離)
Voronoi セルの境界までの距離。
出力はDistanceのみです。
- Distance…Voronoi セルの境界までの距離。

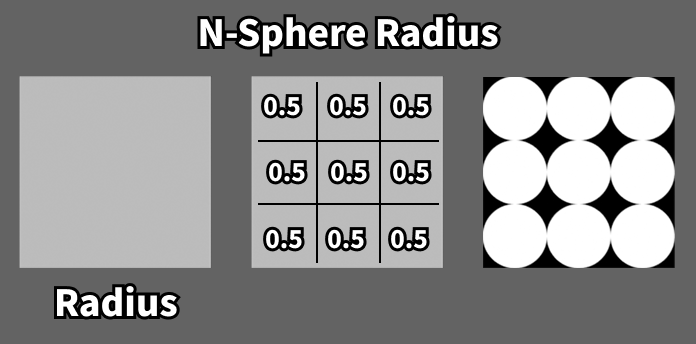
N-Sphere Radius (N球面半径)
Voronoi セルに内接する n 次元球の半径。つまり、最も近い特徴点と、その次に近い特徴点との距離の半分の値がそのセルに入っています。
出力はRadiusの値のみです。
右図は、ランダム値0だと、同じ値が全てのセルに入っているためグレー1色に見え、それをF1の閾値にして球の半径として使うと内接する円を描けるという参考図です。
Voronoi Textureの基本パラメータ
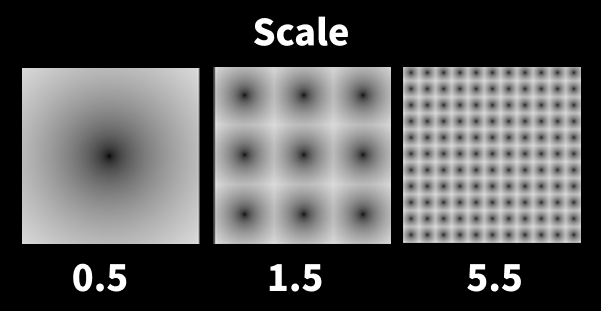
Scale
セルの大きさを決めます。数値を大きくするとセルは小さくなっていく
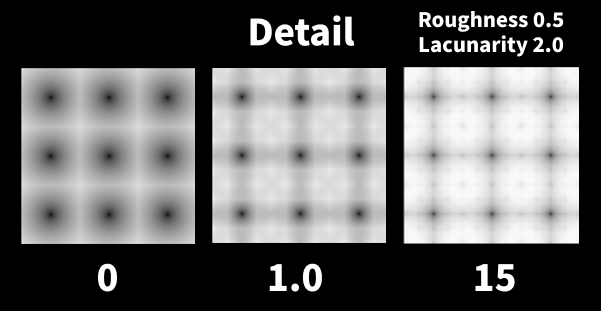
Detail (細かさ)
ノイズのオクターブ数。
入力の小数部分は、最も高いオクターブの強度で乗算されます。
オクターブ数が多いほど、計算時間が長くなります。
基本位置にノイズを加えるので空間が歪みぼこぼこになり、単純な計算ではなくなります。
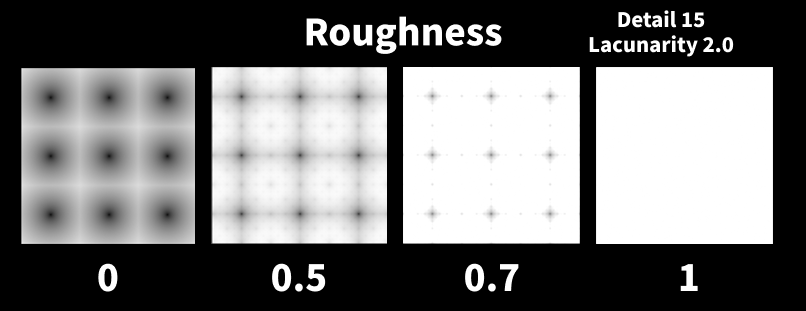
Roughness
より滑らかなノイズパターンと、より荒く尖ったピークのノイズパターンの間をブレンドします。
Detailでノイズを入れないと効果はありません。
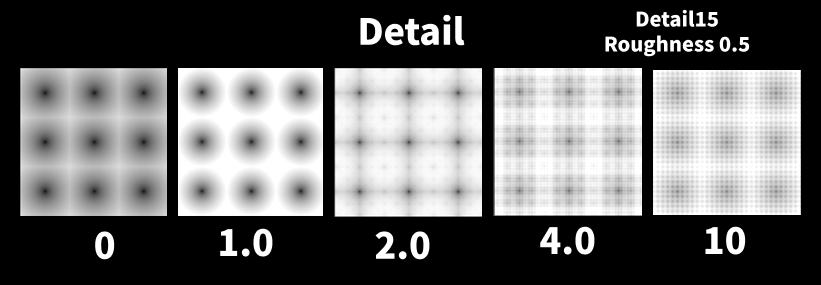
Lacunarity
各オクターブ(ノイズの階層)が前の階層に比べてどれだけスケール(細かさ)が大きくなるかを決める値です。値が大きいほど高いオクターブ(細かいノイズ)がより細かく・複雑になる
Randomness
特徴点の位置がランダムに散っていきます。3Dや4Dのモードだと、特徴点が上下方向にも散るので、F1でも特徴点の黒い点が平面に見えなくなったりします。

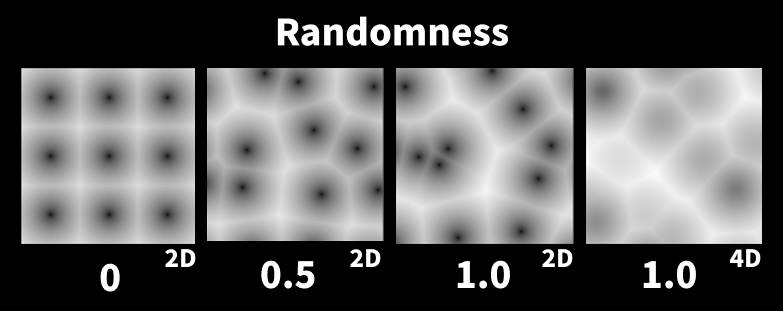
Smoothness(Smooth F1使用時)
- セルの境界線の滑らかさ
- ひび割れ感をなくして、境界をなめらかにする
Distance Metric (距離関数)
テクスチャの計算に使用される距離の計算方法。距離を測る計算方法は実は1つではなく、いろいろな測り方があります。測り方を変えることでできる形が違い、ユニークなパターンが生成されます。
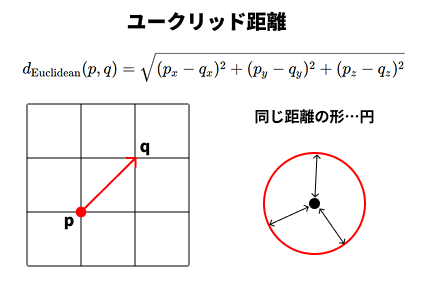
Euclidean (ユークリッド距離)
私たちが一般的に使っているユークリッド距離を使用するモードです。もっとも一般的な距離。座標間の「直線距離」です。
右図のように、私たちが日常的に使っている距離です。点pと点qの距離は、一本線を引いて、その線の長さを求めます。
ある点から同距離の点を集めると円になります。
特徴
できる形…円(ball shape)
→ 等距離は完全に丸い
ドットなどのパターンを作ることができ、カラー成分もあるのでカラフルな柄を作ることができます。

細胞のような形ができる
Voronoi(Euclidian)は、特徴点から距離が広がり、お互いの“成長領域”がぶつかる場所で境界ができます。
これは細胞や泡が膨らんで隣と押し合い、自然に区画ができる仕組みにそっくりなため、生物的・自然的なパターンが生まれます。
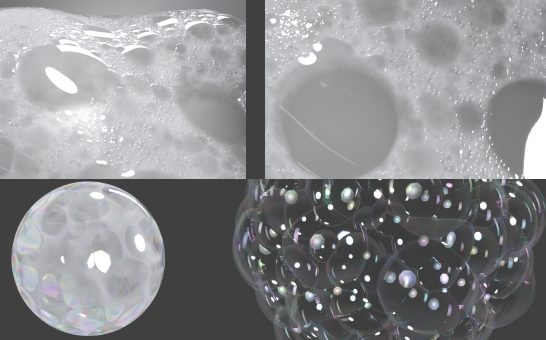
右図 細胞ぽい形、キリンの柄

右図
上 大小の円を重ねて作った泡
左下 3Dでセル境界をvolumeで可視化したもの
右下 セルを膨らませて作った泡の形
スムーズF1を使ってセルの境界を滑らかにすることができ、河原の石のような形を作ることができます。
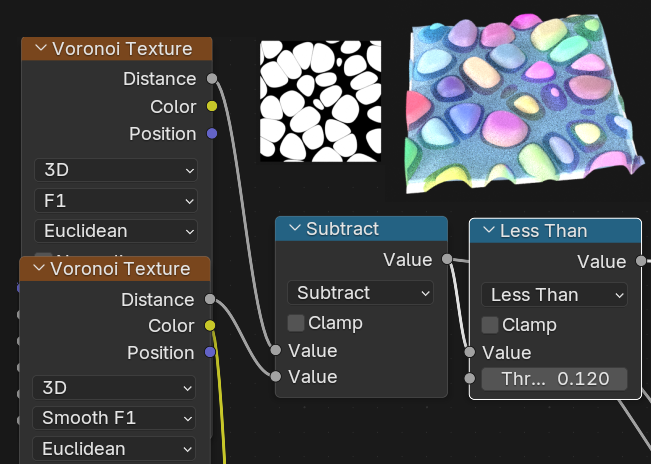
石垣の形…境界はDistance to Edgeの形。
石のテクスチャ…石のボコボコ感を表現できます。
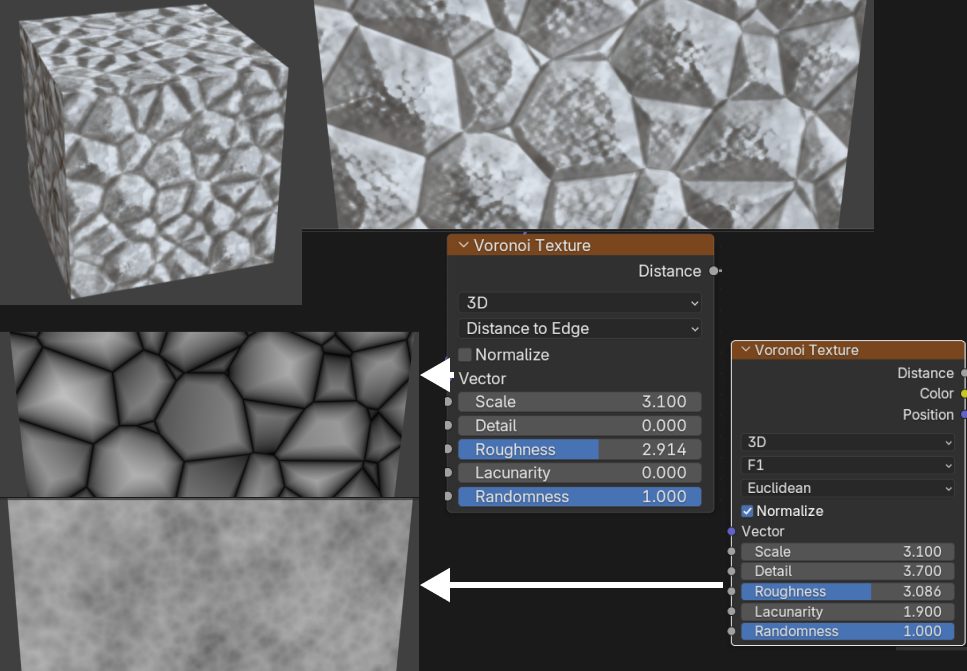
Manhattan (マンハッタン距離)
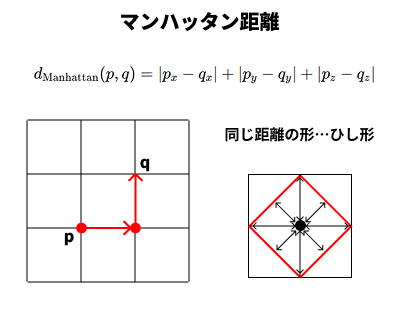
道路のブロックのように「縦+横+高さ」で距離を測る方法。
例えば右図でいうと点Pと点qはX方向に1,Y方向に1離れていますので、距離は1+1=2です。近道とか斜め歩きはできません。
京都みたいに縦横に道が伸びていて、碁盤の目のようなグリッドになっている街ではこういうふうにしか進めないですよね。マンハッタンもそんな街らしく、距離の名前の由来になっています。
ある点から同距離の点を集めるとひし形になります。
特徴
できる形…四角い・直線的・格子状・ひし形
Euclidian が「円が広がってぶつかる」イメージなのに対し、
Manhattan は “十字型の波” が広がってぶつかるイメージです。
- 上下左右方向へ距離が伸びる
- 斜め方向は遠めの距離が出る
- ひし形や四角形、直線の形がよく出ます。
結果として、
道路の区画・街区・デジタルな格子のような形が自動的にできあがります。

SmoothF1があるので、少し丸みを帯びた形もできます。正方形から曲線までできるので使用範囲が幅広いと思いました。
街並み・道路・区画のパターン
Manhattan は街区の距離計算が語源なので、
都市的・人工的なパターンが作りやすいです。
- 簡易的な都市マップ
- 街灯、区画線のランダム配置の基盤
などに使えます。

デジタル・電子回路・サイバー感のある模様
境界が直線なので、基板のような硬質パターンになります。
- サイバーパンクのパネル模様
- 回路パターン
- デジタル系の背景
- ローポリの人工オブジェクトのざらつき
など、人工感の演出に最適。

サイバー壁、sci-fiパネルみたいなパターン。
SmoothF1(F1でもできます)で色面をわけて、Bumpノードで凹凸をつけます。Filter Widthで溝の表現がはっきりしてきます。
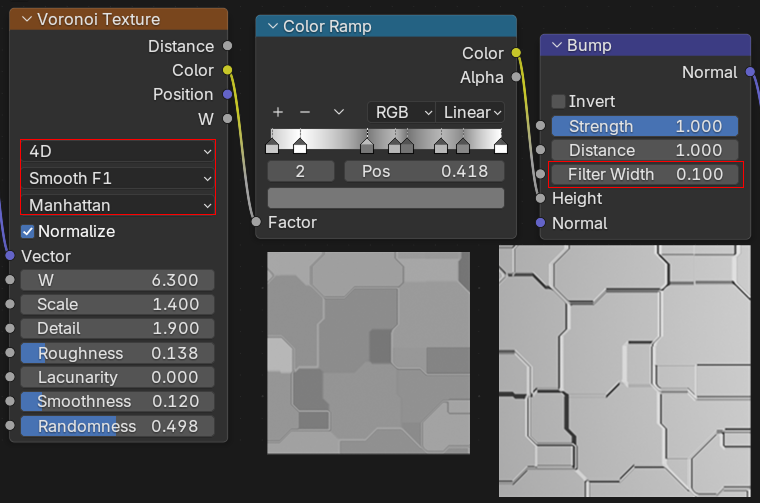
タイル・市松模様などの規則パターン
自然物には使いにくいですが、
タイル・床材・人工の石張りなどには相性が良いです。
(正方形を扱いたい場合はチェビシェフを使った方が楽かもしれません)

紙などの素材
DetailやRaghness,Lacunarityを上げていくと、シャープな線が重なったような繊維系の素材のテクスチャができます。
- アルミホイル
- 壁
- 和紙
- 紙・クラフト素材
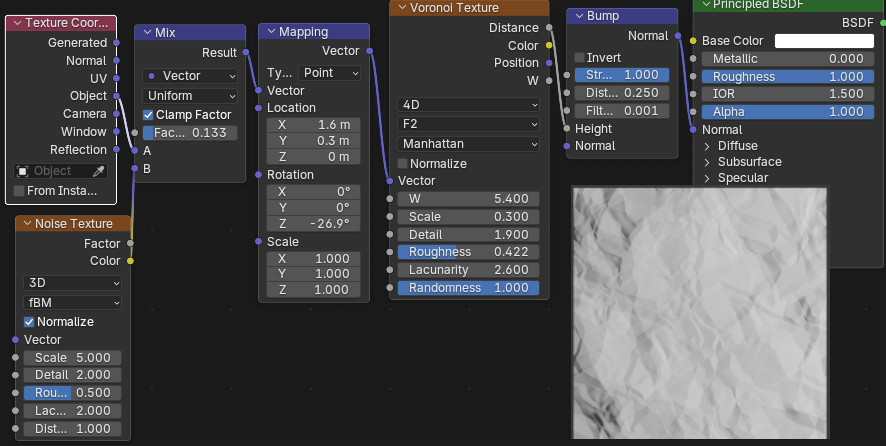
アルミホイルの右の図はアルミホイルを作るときの元のボロノイ図のカラーです。

紙のノードは右図のようになっています。
座標にノイズを加えて少し曲げています。
Chebychev (チェビシェフ距離)
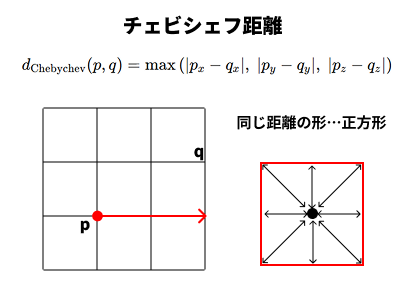
差分の中で 最大の軸差 が距離として使われる方法。「x方向の距離」と「y方向の距離」のうち、大きい方が距離になります。
右図でいうと、点Pと点qが、X方向に2、Y方向に1離れていますね。そういうときは距離は2となります。初めて知った方は、そんなん距離じゃねぇ‼適当すぎるだろ‼って思うかもしれませんが、そういう距離の測り方なのです。
ある点から同距離の点を集めると正方形になります。
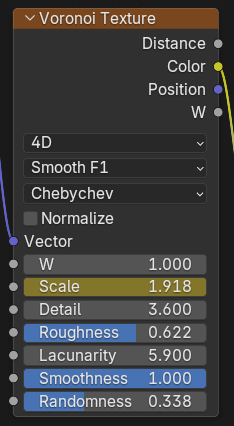
特徴
できる形…完全な四角形(立方体)セル・正方形(最大成分だけが距離を決めるため)
- 完全に四角形の領域になる
- グリッド感が強く、硬くて機械的な見た目
- パターンが均等で「ドット・ピクセル風」になる
- Manhattan よりもさらに人工的で硬い形
機械的・デジタル・タイル状の模様に向いてる。ほぼマンハッタンと一緒の特徴があるけど、4Dモードなどにしたとき、ランダムで動かすと四角形が前後に重なるという違いがあります。

チェビシェフノイズのアニメーション
Voronoiもノイズやざらついた質感を表現することができ、Scale値を変えると少しホラーな表現ができるなと思いやってみました。
チェビシェフの場合基本が正方形なので、紙がちぎれたような、ドットやピクセルが欠けたようなラフな表現ができます。
Minkowski (ミンコフスキー距離)
今まで説明した距離をすべて含む「一般化された距離」。
指数(n)によって振る舞いが変わる。
右図の数式のnの値が変わっていきます。以下は指数nが特定の値になったときにどんな距離になるかを表したリストです。
- 指数 1のとき → Manhattan 距離
- 指数 2のとき → Euclidean 距離
- 指数 → ∞(非常に大きい値)のとき → Chebychev 距離

特徴
できる形
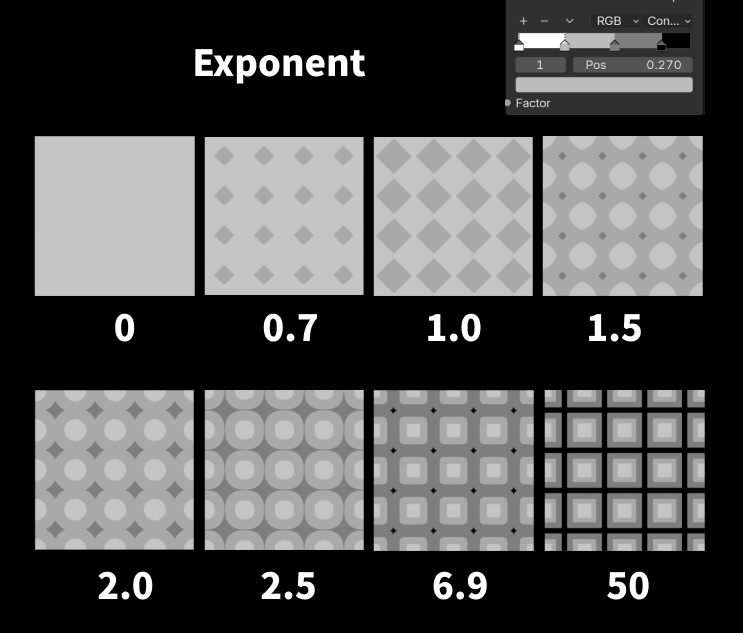
指数 (Exponent)n を変えると形が滑らかに変化する。
n = 1 → Manhattan
→ ひし形
n = 2 → Euclidean
→ 円
n = ∞ → Chebychev
→ 正方形
n を連続的に変えると?
ひし形 → 丸 → 四角
という風に形が徐々に変化する。
ダイヤ→丸→四角へ滑らかに補間される
アニメーションやパラメトリックな表現に使うことができます。
様々な形
今まで紹介した形の性質を内包しているため、かなり多様な形を作成することができます。
特徴的なのは、丸から四角など、曲線から直線的な形へ変化する歪みやいびつさが簡単に表現できるため、このような効果が好きな人にはオススメです。
また、Exponentが1以下のときに細い線のような形が出てくるので、繊維的な表現もできます。

形状を変えるアニメ
Exponentを増やしていくと、だんだん距離が伸びていくので、セルが外側に広がり、柔らかくぶつかるような表現ができます。
Voronoi Textureノードの使い方のポイント
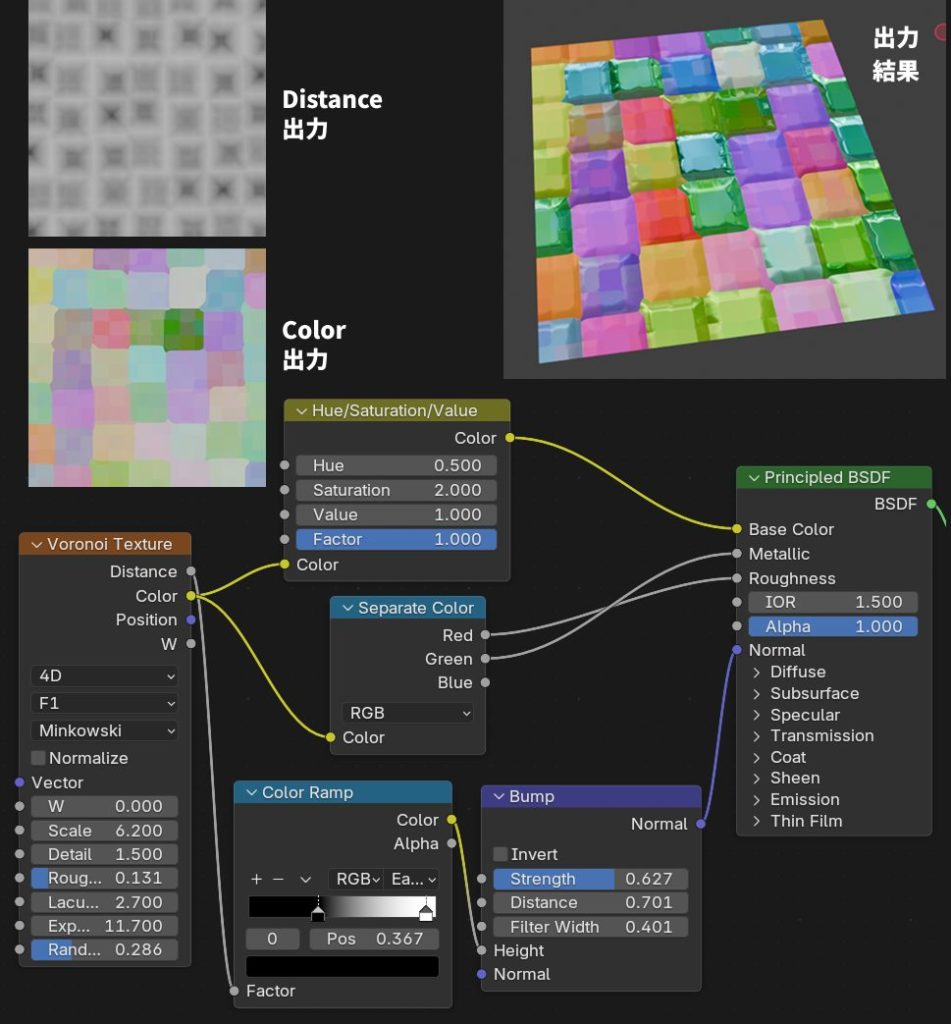
Voronoiテクスチャノードは様々な出力があります。それぞれの出力を組み合わせて使うことで面白い表現やテクスチャができます。
右図を例に説明すると、
Distance出力をノーマルマップの値として、
Color出力をベースカラー、また、RGBに分解して、さらにMetallicなどの値として使っています。
他にもFeature (特徴出力)やDistance Metric (距離関数)のモードを変えて複数のノードを組み合わせることで多彩な表現ができます。
描画シェーダー
これらの効果を組み合わせることで描画シェーダー、筆致テクスチャなどとして使えます。
オブジェクトに使うことで油絵風やイラスト調の描画シェーダーのテクスチャとしても使えます。
ボロノイテクスチャを使ってBlenderで絵を描いてる方もいます、そのくらい2D表現とも相性がいいテクスチャです。
以下の記事でノード構成など解説しています。

まとめ
- Voronoi Textureは「距離」で模様を作る特殊ノイズ
- モードを変える組み合わせで多様なパターンが作れる
- Color出力は抽象模様、Distance出力は質感付け向けなど、出力を組み合わせて使う
自分はあまり質感にボロノイテクスチャって使ってこなかったんですが、今回いろいろ勉強してみてめっちゃ使えると実感しました。
今まで使ってみて、ノイズテクスチャよりどういう模様が出るか推測しにくくて使いにくい…というか、普通に距離の計算の話が出るので難しいと思うんですよね。今回一応図解してどういうパターンが出やすいか解説してみたんですが、どうでしょうか。なんとなくこういうパターンが出るかな…?っていうのが推測しやすくなってればいいな。
あとは、カラーとDistanceの出力を使い分けて、組み合わせるのも大事だなと思いました。スケールを変えて組み合わせたり、重ねることで実力を発揮していくテクスチャだと思いました。
ぴんとこないなーと思う方も、距離の計算など原理を知ったあとに使っていくと、できる形も把握できてくると思います。描画シェーダーや絵画、イラスト調など2Dの表現にもかなり使えるテクスチャで、実験するだけでも楽しいので、ぜひ触ってみてください!!
関連記事
マテリアルシェーダーで質感やパターン作りに関連した記事まとめ




コメント