Blender 5.0 のジオメトリノード、 Repeat Zone を使うと、「同じ処理を何度も繰り返す」ことで、驚くほど複雑な形状を簡単に作れるようになります。
この「繰り返し処理」と非常に相性が良いのが、フラクタル図形です。
シンプルなルールを何度も適用するだけで、まるで自然物のような複雑な模様や構造が現れます 。
この記事では、Blender 5.0 の Geometry Nodes(ジオメトリノード) にある Repeat Zone を使って、
- シェルピンスキーのギャスケット、ピラミッド(Sierpinski gasket/pyramid)
- シェルピンスキーのカーペット(Sierpinski carpet)
- メンガーのスポンジ(Menger sponge)
- フラクタルツリー(Fractal Tree)
- オリジナルのフラクタル図形
といったフラクタル図形を、ノードで作っていく方法を解説します。
「フラクタルって難しそう…」
「数学はちょっと苦手…」
という方でも大丈夫です。 難しい式は出てきません。
Repeat Zone の動きと考え方に注目しながら、「どうしてこの形になるのか」を一緒に確認していきましょう。

この記事は、Blenderのジオメトリノード、Repeat Zone(リピートゾーン)を使ってフラクタルを作る方法について解説している初心者~中級者向けの記事です。
難易度
フラクタル図形とは?
フラクタル図形とは、
全体と部分がよく似た形をしているという特徴を持つ図形のことです。
代表的な特徴は、次のようなものです。
- 拡大しても同じような模様が現れる
- 非常に単純なルールから作られる
- 繰り返し処理(再帰・反復)によって生成される
たとえば、シェルピンスキーのカーペットは、
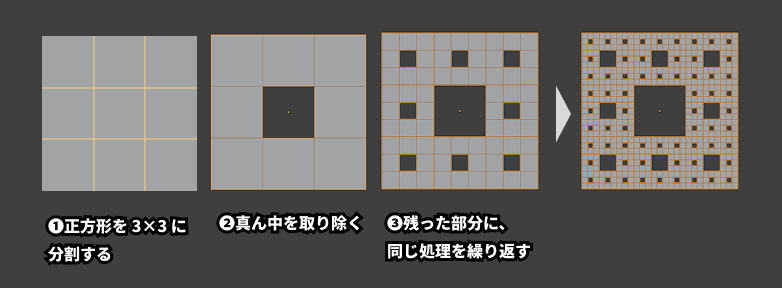
- 正方形を 3×3 に分割する
- 真ん中を取り除く
- 残った部分に、同じ処理を繰り返す
という たった3つのルールから生まれます。
Repeat Zone は、まさにこの「前回の結果を次の処理に渡しながら繰り返す」というフラクタルの考え方を、そのままノードで表現できます 。
ちなみにRepeat Zoneノードの使い方がよくわからないという方はRepeatノードの基礎について解説した記事がありますのでぜひ読んでみてください。初心者だといきなり使うのは難しいかもしれません。
シェルピンスキーのギャスケットを作る
ではさっそくシェルピンスキーのギャスケットを作ってみます。
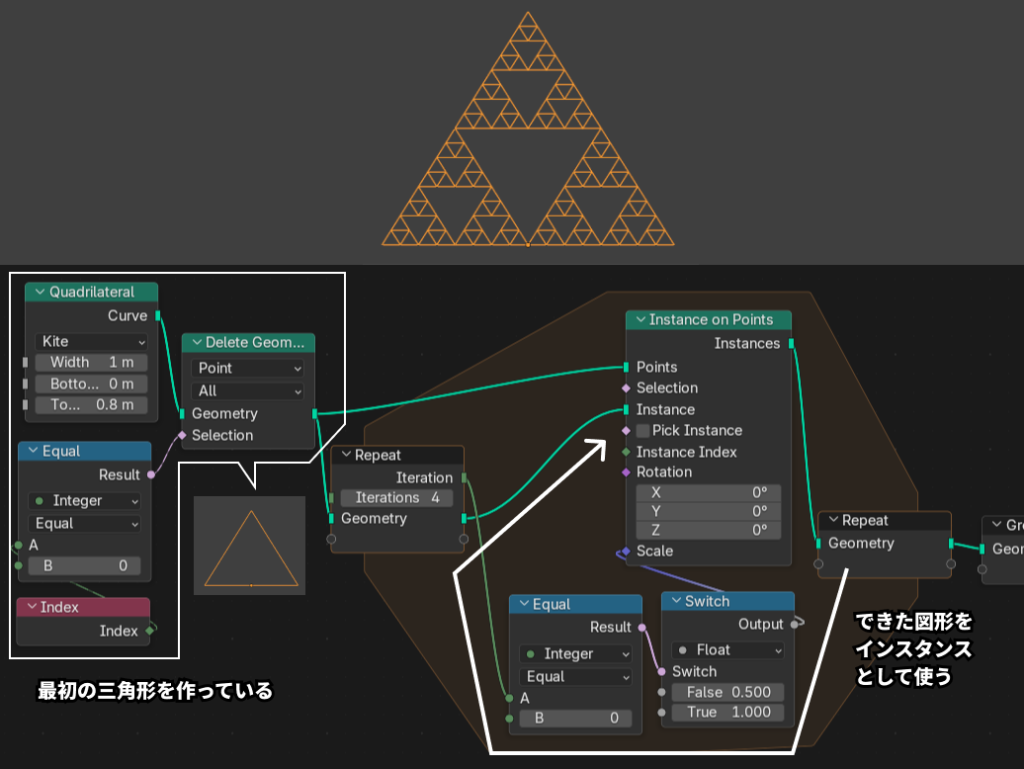
全体のノード構成は以下の図のようになります。まずとにかく三角形のカーブをリピート入力ノードに入力します。今回はQuadrilateralノードのKiteモードを使って1点ポイントを削除することで最初の基本となる三角形を作っています。三つ頂点の三角形ならなんでもいいです。
Repeat Zone内部でInstance on Pointsノードを使って、最初の三角形を外部からポイントに入力します。Instancesの出力をリピートの出力ノードに接続し、入力ノードから出てきたものをInstanceにつなぎます。
何が行われているのか
ノードだけ見てもわからないので、どのような原理でできているのかリピートの回ごとに解説します。
※シェルピンスキーのギャスケットはカーペットと同様に、三角形を分割して中心をくり抜くという作業を繰り返してできる図形ですが、Blenderではくり抜きよりインスタンスを配置する方法の方が簡単なので、オリジナルのフラクタルの作り方とは違う方法で作成しています。
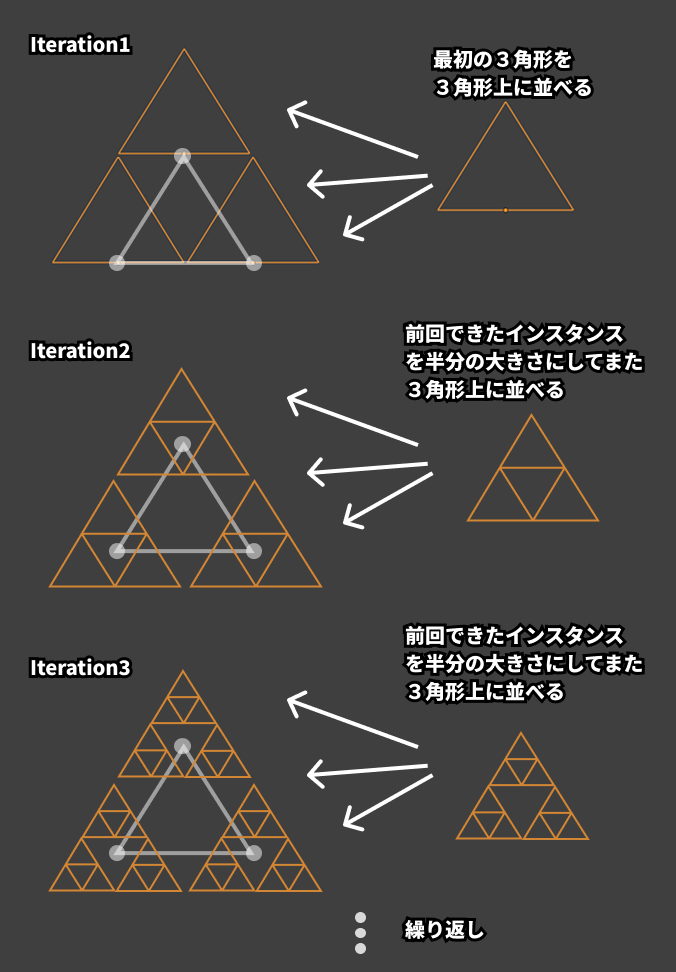
- Iteration1…最初の三角形の3頂点上に同じ三角形をインスタンス配置して並べます。(たまたま最初に作った三角形の原点が底辺中心にできていたため、インスタンスを配置するときの基準点が底辺中心になっていますが、原点がどこでも問題ないです。)ここでは同じ大きさの三角形を並べていることに注目してください。
- Iteration2…1回目でできた図形を半分の大きさにして、また最初の三角形のポイント上にインスタンス配置していきます。(iteration1回目では1倍、2回目以降は0.5倍の大きさにして並べる必要があります。ノードの中の、Switchノードで、iteration出力が0だったら(1回目の出力は0になります)という条件分岐でスケールの値を変更しています。)
- Iteration3…2回目で出来た図形を半分の大きさにしてまた最初の三角形のポイント上にインスタンス配置しています。
- 以後はこの作業の繰り返しになります。
どんどん三角形が細かくなっていき、複雑で綺麗な図形が簡単に出来上がります。
シェルピンスキーのピラミッドを作る
シェルピンスキーのピラミッドはギャスケットの立体版です。作り方はほぼ同じで、平面ではなく、3Dの四角すいをベースのジオメトリとして、インスタンス配置して並べていきます。
ConeノードのVerticesを4にすれば簡単に四角すいを作ることができます。
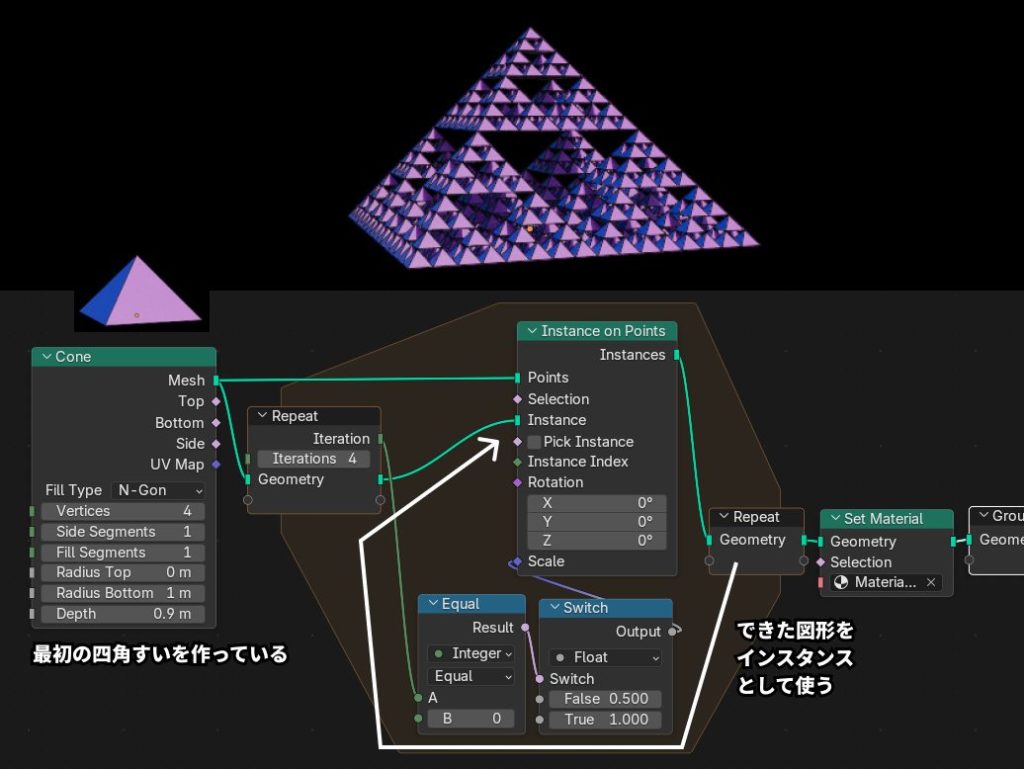
ギャスケットのときは最初の三角形の3つのポイントにインスタンス配置をしていましたが、ピラミッドの場合は四角すいの5つの頂点にインスタンス配置をしていきます。
右図を見ると、部分が1回前の出力全体の形でできていることがわかると思います。

シェルピンスキーのカーペットを作る
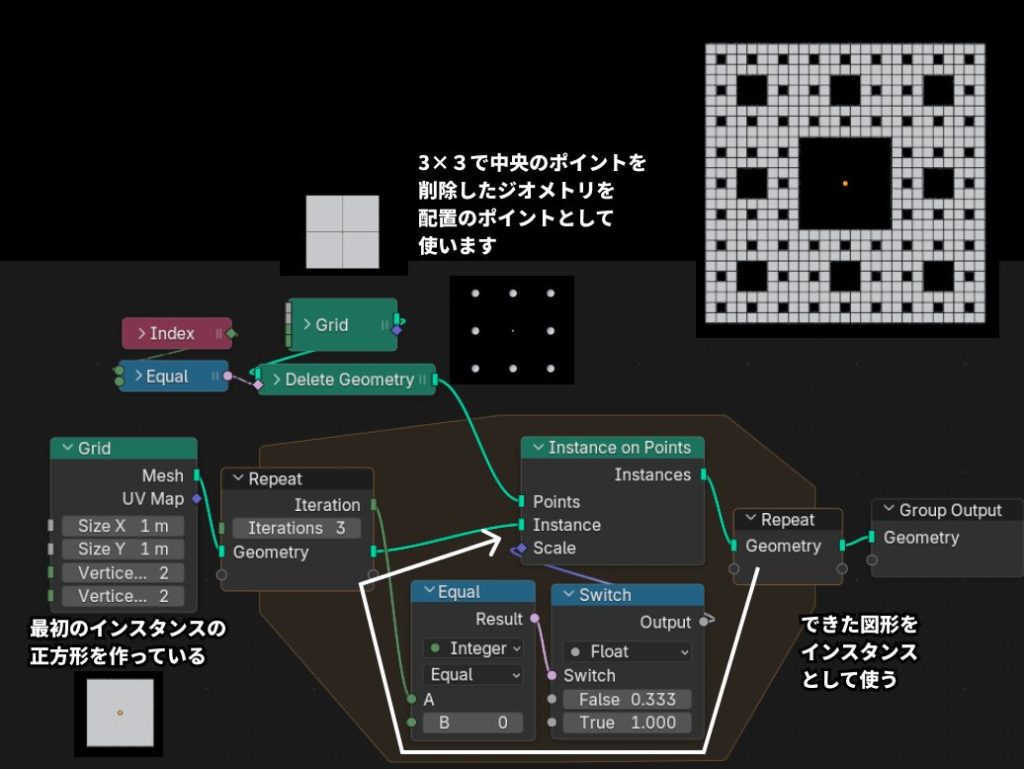
シェルピンスキーのカーペットの基本の形は正方形です。Gridノードで正方形を作りRepeat入力ノードにつなぎます。
Instance on PointsノードのPointsには、3×3の正方形で、中央の頂点を削除したジオメトリを使います。大体の作り方はギャスケットと同じですが、インスタンスとポイントのジオメトリが違います。
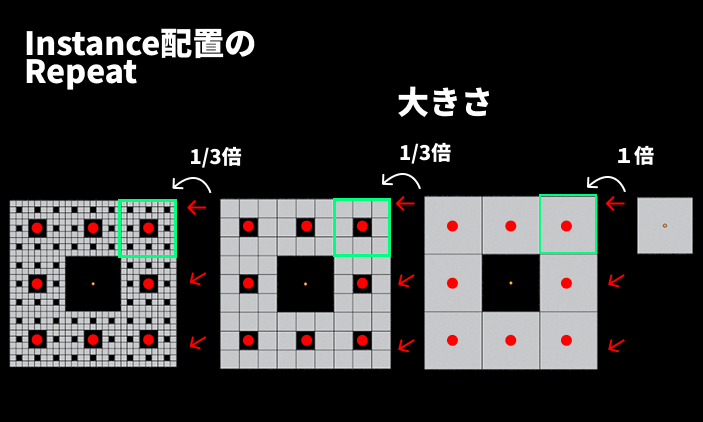
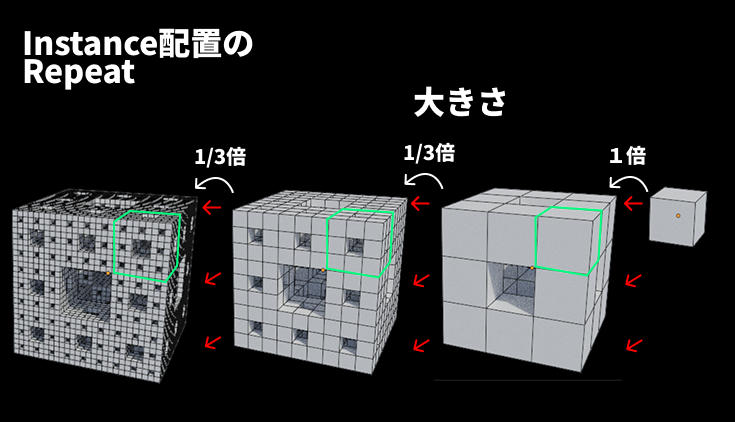
右図はわかりやすいように、各リピート回数で出力されたジオメトリの大きさの比率をそのままにして表示しました。
最初は1倍の大きさのまま各ポイントに配置しましたが、次回以降のリピートでは1/3倍してインスタンス配置する必要があります。
初回は1倍、次からは1/3倍という場合は、Switchノードを使うと、Iteration出力に応じて出力する値を出しわけることができます。
※ここで注意すべきなのは、1回目のiteration出力は0になるということです。
メンガーのスポンジを作る
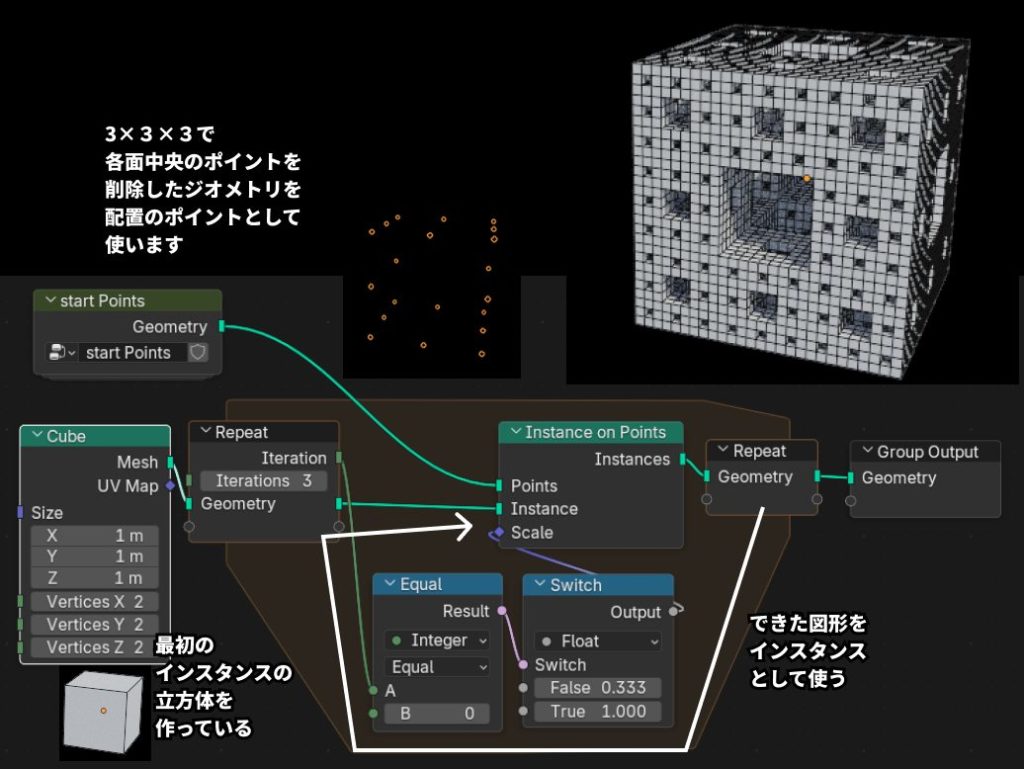
メンガーのスポンジはシェルピンスキーのカーペットの立体版です。作り方や考え方はほぼ一緒です。
基本のジオメトリは立方体で、それをRepeat入力ノードに接続します。Instance on PointsノードのPointsには、3×3×3で各面の中央頂点を削除したジオメトリを入力しています。
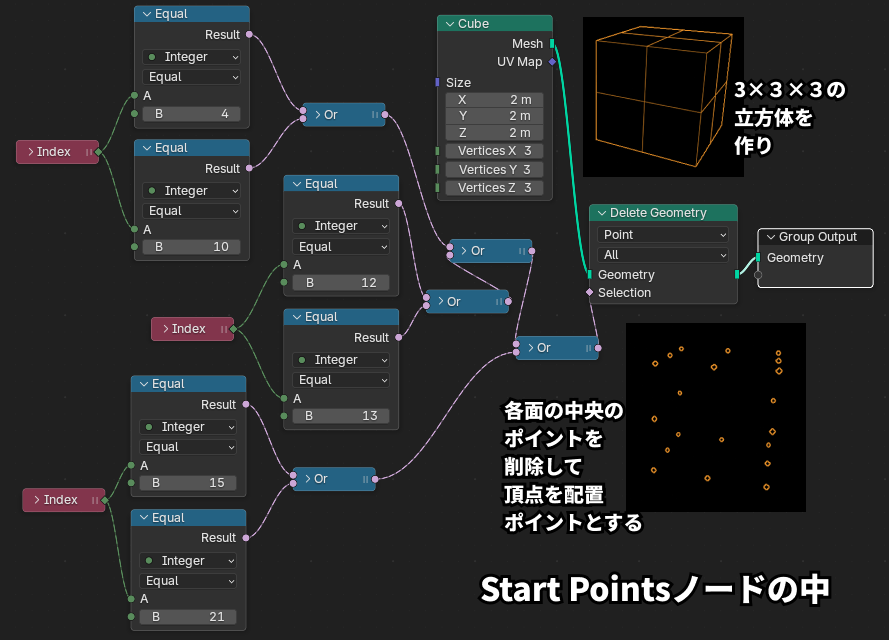
Start Pointsノードの中身
右図がインスタンス配置ポイントとなるジオメトリの作り方です。
頂点が3×3×3の立方体をCubeノードで作成し、Deleat Geometryノードで各面の中央ポイントを削除しているだけです。
右図はわかりやすいように、各リピート回数で出力されたジオメトリの大きさの比率をそのままにして、インスタンスがどのように繰り返し配置されているか示した画像です。
最初は1倍の大きさのまま各ポイントに配置しましたが、次回以降のリピートでは1/3倍してインスタンス配置する必要があります。
初回は1倍、次からは1/3倍という場合は、Switchノードを使うと、Iteration出力に応じて出力する値を出しわけることができます。
※ここで注意すべきなのは、1回目のiteration出力は0になるということです。
フラクタルツリーを作る
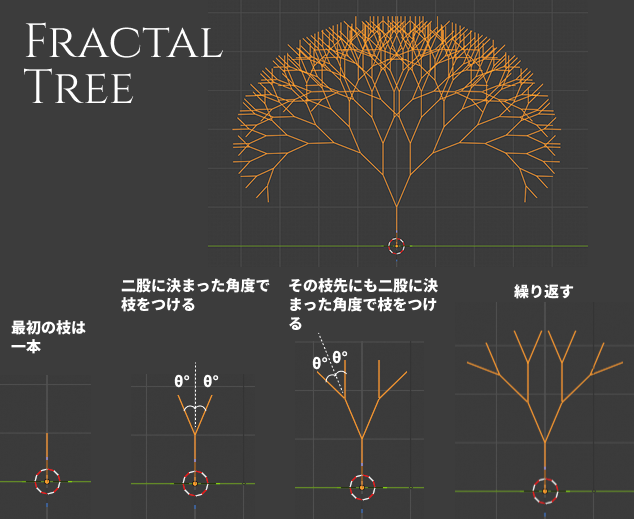
フラクタルツリーとは
一本の枝に、一定の角度で二股に枝をつけていき、その枝先にも同じ角度で二股に枝をつけていくことでできるフラクタル図形です。
Blenderでも同様に特定の角度で枝を二股につけていく処理はできますが、ちょっとノードが複雑になってしまいます。なので、今回は今までのフラクタル図形制作工程と同様に、できたジオメトリをそのままインスタンスとして再配置していくという手法を取ろうと思います。
全体ノード
フラクタルツリー制作のノードは以下のようになります。わかりやすいように1回目でどのような図形ができあがっているかを図の中に書きこんでいます。
まず最初はただの線をCurve Lineで作成します。基本の枝の形として、左の枝、右の枝用のInstance on PointsノードのPoints入力に直接つないでいます。Instance入力にも入れたいのですが、最初以降は、出力されて出来上がったジオメトリをインスタンスにしたいので、Switchノードで出し分けています。
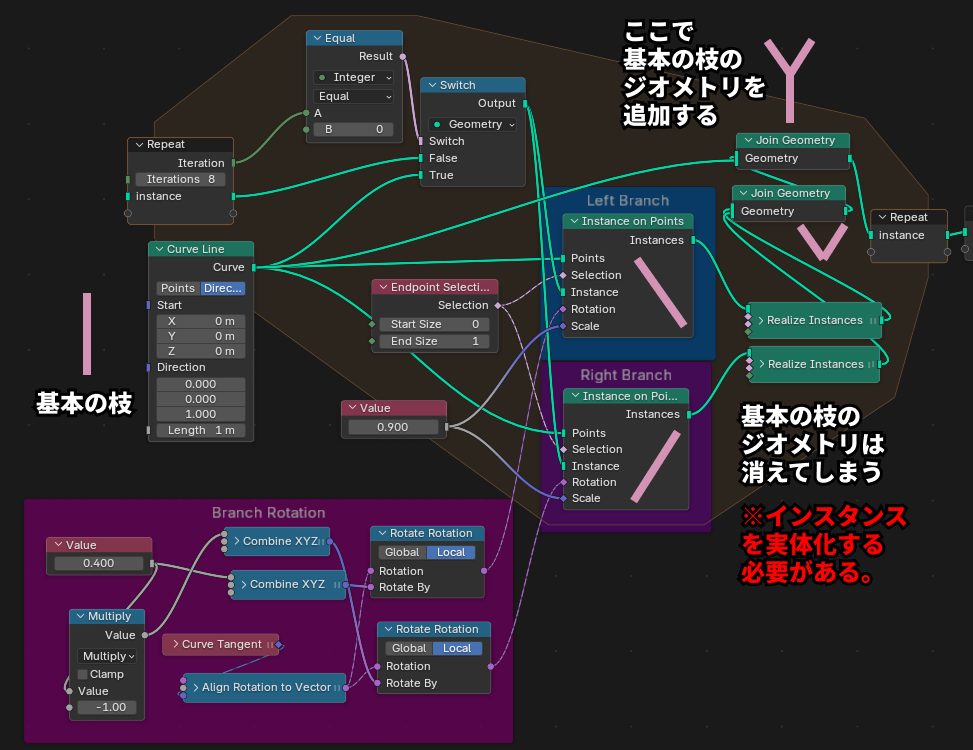
ポイントとしては、インスタンス出力では、ポイントとなった基本の枝のジオメトリは消えてしまうので、あとからJoin Geometryで追加する必要があるということです。さらに、実体化されてるジオメトリと、インスタンスを混ぜるとうまく表示されなくなるので、インスタンス出力をRealize Instanceで実体化する必要もあります。
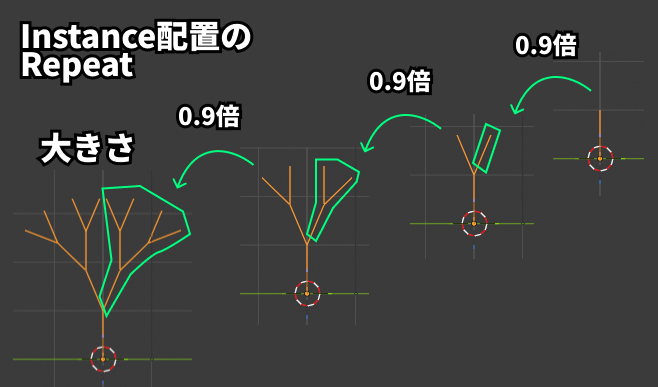
Instance on PointsノードのScaleに0.9を入れ、インスタンスを徐々に小さくしていきます。また、Rotation入力では、Align Rotation to Vectorで枝のラインのCurve Tangentに揃えてから、Rotate RotationでX軸に特定の値だけ回転させ、二股に枝を付けています。
右図はわかりやすいように、どのようにインスタンス配置をリピートさせているかを図示しました。
大きさの倍率や、枝の付き方の角度を変えることでパターンが変わってくるのも面白いです。
オリジナルのフラクタル構造物を作る
これまで見てきたフラクタルはシンプルで簡単な作りをしていました。自分でも簡単なルールを作ってオリジナルなフラクタル構造物・図形を作ることができます。
オリジナルフラクタル
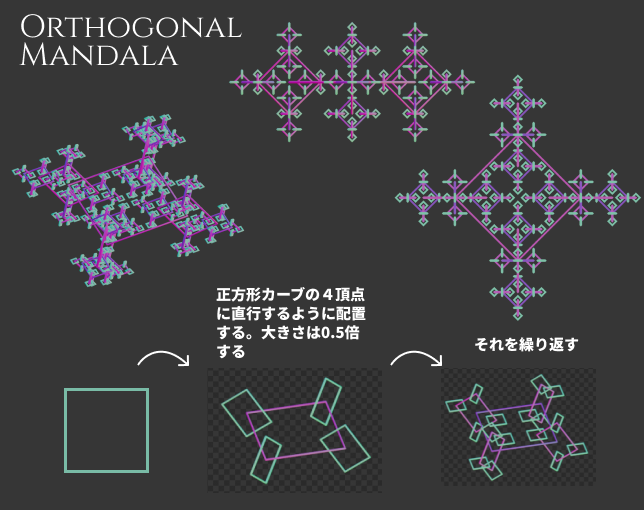
正方形のカーブを使って右図のようなフラクタル構造を作ってみました
ルール
- 最初は正方形のカーブを正方形カーブの頂点に直行するように配置する。大きさは0.5倍する
- できた構造を同じルールで繰り返して配置する
これだけです。
全体のノード
ノードは以下のように組んでいます。今までのものとほぼ同じような作りですが、正方形カーブを追加された順番によって色が変えられるようにStore Named AttributeノードとRandom Valueノードを使っているところがポイントです。
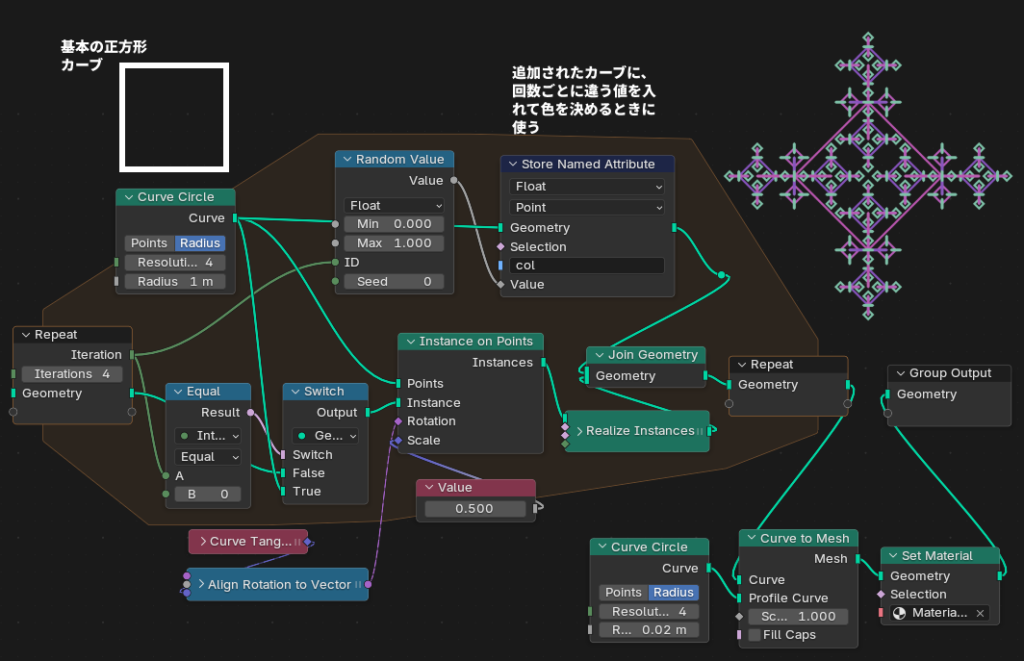
ノードを組んで実行してみると、予想もしていなかった面白い図形が現れてきます。
オリジナルのフラクタルを作るポイント
フラクタルを作るには、自分で簡単なルールを作ってそれを繰り返すことが重要ですが、ルールと言っても最初はわかりにくいので、
- 基本のジオメトリを決める
- 配置のルールを決める(移動、回転など)
- リピートによって大きさを変える
これらに気を付けて作ってみることをオススメします。Repeat Zoneノード内でInstance on Pointsでインスタンスを使って循環させると、わりと簡単にフラクタルを作ることができます。
ポイント:リピート回数によって色を変えるとわかりやすいし綺麗になります。
Blender × フラクタルの面白さ
Blender を使うと、フラクタルは「数学の図形」から実際に触れる 3D 形状へと変わります。
- 反復回数を変えて形の変化を見る
- ノードを少し変えてオリジナルのフラクタルを作る
- マテリアルやアニメーションと組み合わせる
といったことも簡単に試せます。
特に Blender 5.0 の Repeat Zone は、
- 「なぜフラクタルができるのか」を理解しやすい
- シェーダーや数式的な考え方にもつながる
という点で、学習にも表現にも非常に強力です。
まとめ
フラクタルという図形を知ったときは、その不思議な形と構造に惹かれて、どうしても自分で作ってみたいと、シェーダーやノードなどで頑張って作っていました。
フラクタルのことを初めて知った、と言う方になるべくおもしろく伝えられたらいいなと思ってまとめてみましたので、ぜひ自分の手で作ってみてほしいし、その面白さを実感してほしいです。なんだかよくわからない、という方でもBlenderのノードで作ると頭というより、手や視覚で理解しやすくなると思います。
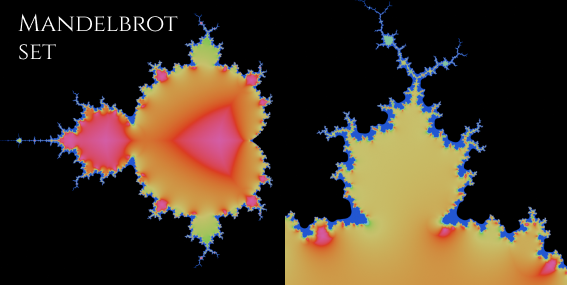
また、フラクタル図形には、複素数計算によるマンデルブロ集合(Mandelbrot set)や、それを発想の元にした立体フラクタルであるマンデルバルブ(Mandelbulb)などもあります。
シンプルな計算式から、無限に続く奇妙なパターンが出てくる面白い図形です。
機会があれば記事を書いてみたいと思います。
関連記事
リピートノードについて基礎的な使い方を詳しく解説しています。



コメント