Blenderで植物を作るとき、適当に作ってもリアルでいい感じに見える葉の配置について発見したので書いておきます。
少ない葉でも自然に見えるポイントは「互生の螺旋配置」と「137.5°の回転角」です。
この記事では、まず簡単にその作り方を紹介し、後半でなぜ自然に見えるのかを解説します。
※この記事は、Blenderである程度制作経験があり、見た目の「自然さ」の理由を理解したい人向けの記事です。
Blenderで自然に見える葉の配置
Blenderで植物を作るとき、葉の配置って悩みますよね。
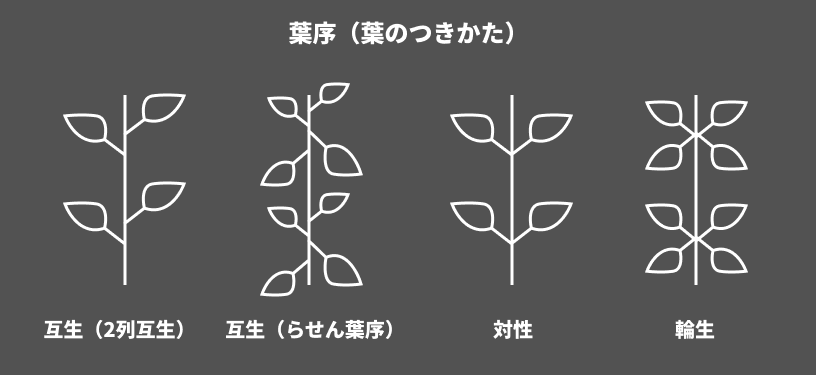
少ない葉でも自然に見える配置は「互生の螺旋（ねじれ）配置」です。
回転角：137.5°（黄金角）
各葉を前の葉から137.5°ずつ回転させて配置すると、バランスよく広がります。
重ならず、少ない葉でも自然に見えるのがポイントです。
Blenderでの簡単実装例（Geometry Nodes）
ジオメトリノードで葉の付き方を設定していきます。
- 葉のインスタンスを用意する
Instance on Points ノードで葉を配置 - 回転を設定
Rotate Instances ノードで Z軸に 137.5° × Index ÷ ラジアン
を入力 - 完成
少ない葉でも自然に広がる螺旋状の配置が完成！
ポイント：葉の数やスケールを調整するだけで、さらにリアルになります。
詳しく解説
葉の配置には、インスタンスの回転を使います。この際、インデックスを参照して各葉を回転させることができます。ここで入る数値はラジアンなので、indexで0,1,2,3…と入れていくと１ラジアン（約57.3°）入ってしまっています。そこで黄金角約137.5°を１ラジアン分の約57.3°で割った比率をかけると、インデックス順に黄金角に従った葉序を設定できます。
葉の数が少なくても多くても、バランスよく配置できるので便利な方法です。
めんどい方は2.4をIndexに掛けてください。葉の数が少ないならある程度機能します。
他の配置との比較
他の配置の仕方もみて、黄金比での配置がいかに自然か確認してみてください。
等間隔で回転
右図はただindex番号をラジアンとしていれている葉の付き方です。
57°くらいの間隔で葉が回転ている配置ですね。なので詰まってる感じというか、規則的すぎて不自然です。葉の枚数によってはバランスが悪くなるしあまり良くないです。
ランダム配置
これはランダムな配置です。
数値はRadom Valueノードから0～tau(360°)をいれています。かなり重なっていてバランスが悪いです。
完全にランダム性にまかせても自然にはなりません。
以下はなぜ137.5°なのか？黄金比とは何か？なぜ自然に見えるのかなどの踏み込んだ解説です。知りたい方だけどうぞ。
なぜ137.5°なのか？
この角度は「黄金角」と呼ばれ、自然界の植物でよく見られます。
- 葉が重ならず、すべての日光を効率よく受けられる
- フィボナッチ数列や黄金比と関係している
- 実際の植物でもこの角度で葉や花弁が配置されることが多い
これだけ知っておけば、Blenderで自然な葉配置を作ることができます。
葉序について
植物における葉の付き方や配置の様式のことを葉序といいます。
記事冒頭で言っていた「互生の螺旋葉序」とは、植物の葉が茎の周りにらせん状に規則正しく配列する並び方です。
このような植物はより多くの葉に日光を当てるため、フィボナッチ数や黄金角などを利用した葉の付き方が見られます。
なぜ葉序は黄金角になるのか
現実の植物は、葉が日光に当たりやすいように、葉序が黄金角（螺旋葉序の場合）に近づくことが多いと言われています。そもそも「葉序が黄金角に近づく」とはどういう意味でしょうか？
自然の植物は一定の間隔で葉を出して上に成長しています。茎の周りにある角度で葉を出していき、何周かすると最初の方に出した葉と同じ場所に重なります。
同じ葉の場所に重なる前に何週したか、葉は何枚つけることができたかで葉序を表していきます。
例えば１週の間に葉が２枚つく植物は1/2葉序、2週の間に葉が5枚つく植物は2/5葉序、と言われます。
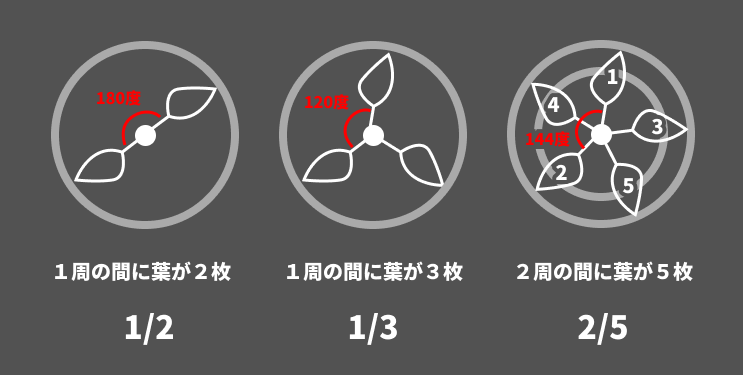
これを小さい順に並べると、葉序のパターンは次のような数列になります。（「互生の螺旋葉序」の場合です）
1/2、1/3、2/5、3/8、5/13、8/21…
これらは、1, 1, 2, 3, 5, 8, 13, 21…というフィボナッチ数列が分子や分母に現れた分数です。なぜフィボナッチ数列が現れるのでしょうか？
以下でフィボナッチ数列と黄金角のつながりについて見ていきます。
黄金角とは
まず、黄金角とは何か詳しく見ていきます。
黄金角は、「黄金比に基づいて360度を分割した角度」です。
こう言われてもよくわかりませんね…。黄金比とは何でしょうか？
黄金比とはフィボナッチ数列（１、１、２、３、５、８、１３、２１、…）の項を一つ前の項で割った数が次第に収束していく数φを使ってできる比率です。
2÷１ ＝2
3÷２ ＝1.5
５÷3 ＝1.667
…
これを∞項までやると出てくる数値が1.618…という無理数φです
黄金比とは、フィボナッチ数列から出てくる無理数φを使った比率で、「１：1.618…」です。（1：φとも書きます）
黄金比がわかりましたので、黄金角を求めていきます。
黄金角とは360度を1：φで分割した1側の角度（約137.5°）です。
黄金角は、黄金比に基づいて360度を分割した角度（約137.5°）です。
葉序と黄金角のつながり
ではさっきの葉序 1/2、1/3、2/5、3/8、5/13、8/21…
とフィボナッチ数列 １、１、２、３、５、８、１３、２１、…
と黄金角 360×１/(１＋φ) の数字にどのようなつながりがあるのか見てみましょう。
例えば葉序２/５のとき、２周（360°×２）の間に５枚の葉が出ているので、葉の間隔の角度を出す計算は360×2/5となります。
この２/5の形を変えていきます。分子を１にすると1/(5/2)となり、さらに変形すると１/(1+3/2)となります。
他の葉序も計算していくと
葉序2/5 = １/(1+3/2)
葉序3/8 = １/(1+5/3)
葉序5/13 = １/(1+8/5)
…
青文字で書いたところの数値が、フィボナッチ数列の項を一つ前の項で割った数になっており、これが続くと黄金比で出てくる無理数φに収束していきます。つまり、最終的には
１/(1+φ)
に収束していきます。
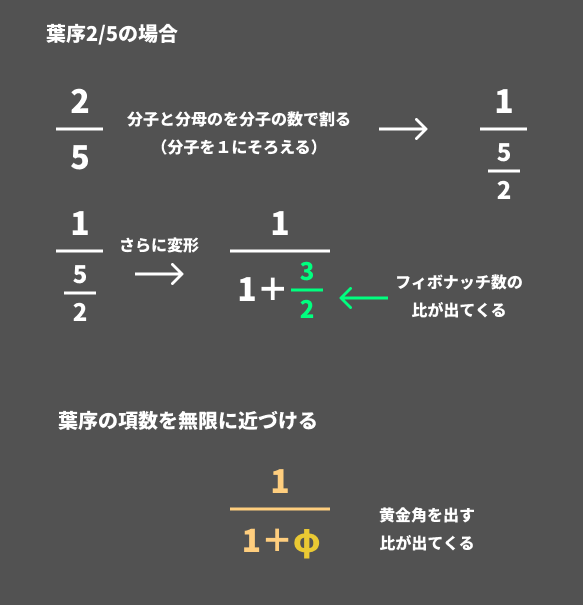
葉の間隔の角度を出す計算は、葉序2/5のときは360×2/5と言いました。この葉序を葉の数を増やしていき、無限枚の葉がつくとすると、最終的に葉の間隔は360×１/(1+φ)となり、黄金角そのものとなります。
この葉序の数列はそもそもどの葉とも重ならないように螺旋のように葉をつけることができることを表しているので、葉の間隔を黄金角にすれば、無限枚（!!）の葉っぱがぴったりと重ならないように配置することができます。
やっと葉序と黄金角、フィボナッチ数、黄金比が全てつながりました。
まとめ：黄金比・フィボナッチ数列の秘密
フィボナッチ数列
数列：0, 1, 1, 2, 3, 5, 8, 13, …
葉や花弁の枚数に多く現れる。連続するフィボナッチ数の比は黄金比に近づきます。
黄金比とは？
約 1:1.618 の比率
フィボナッチ数列から出てくる比率です。建築やデザインで美しい比率として知られる
黄金角とは？
黄金角は、黄金比に基づいて360度を分割した角度（約137.5°）です。
360×１/(１＋φ) で角度を出しました。
フィボナッチ数列は「結果」であって原因ではない
自然の植物を観察すると、葉っぱが重ならない葉序の数列にフィボナッチ数列は出てきます。フィボナッチ数列があって自然が合わせたのではなく、自然の法則の中にフィボナッチ数列はあります。
そしてその自然の法則の中に黄金比や黄金角も存在しています。
植物はそもそも葉の数が増えると葉の間隔を黄金角に近づけていく。そうすればたくさんの葉に日光を当てることができる。そのような機能性が元から備わっています。
黄金比が美しいと言われるのはなぜ？
自己相似性
黄金比の特別さはその自己相似性にもあります。
「全体：大 = 大：小」
という自己相似（スケールが変わっても同じ比）を持ちます。
これは分割しても・拡大縮小しても・どこを切り取っても同じリズムが繰り返されるという性質です。
人間の知覚との相性
黄金比が「美しい」と感じられる最大の理由は、人間の視覚と認知にちょうどよいからです。
1:1 → 単調、安定しすぎ
1:2 → 主従がはっきりしすぎ
1:3 → バランスが崩れる
黄金比は対称ではない（動きがある）しかし不安定でもない「秩序と変化の境界」にあります。
人間は完全な規則 （退屈）→ 完全なランダム（不安）の中間を好みます。
黄金比は「予測できるが、完全には読めない」という位置にあり、人間が満足を得やすい比率になっています。
なぜ黄金比は美しいとされるのか？
✔ 自然と調和している → 最適化の副産物
✔ 「自己相似 × 人間の知覚 × 分布最適化」
Blender制作への応用とコツ
ランダム配置や均等角（90°など）より、137.5°で配置すると自然
葉のスケールや形状を少し変えると、さらにリアル
自然界に忠実にする必要はなく、アートとして調整するのもOK
葉の大きさも線形ではなく二次か三次曲線のようになっていた方が自然に見えます。
作った植物がなんだかリアルにならない、つまらないと感じたら、配置の方法や大きさ、回転角度の規則性を見直してみると良いかもしれません。